M_GP — the weight of the gas-plasma mix;

 M_BK — the weight of the white dwarf;

 M_Iz — the weight of the radiation.

The weight of radiation, concerning the weight of a star, is small and can be neglected in some formulas conclusions, or to be included in the gas-plasma mix weight.

                             M_1GP = M_GP + M_Iz

Then

                             M_Z = M_1GP + M_BK

 The weight of the gas-plasma mix can be defined by the formula

                             M_1GP = M_Z – M_BK                                                                       (5.13)

Let’s substitute the formulas (5.11) and (5.12), in (5.13)

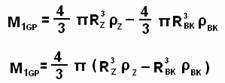
So, we have defined the formulas for calculating the basic parts of a star:

              (5.14)

Since the parameters of the gas-plasma mix define the parameters of the star, we’re interested in the influence of the star’s gravitational field on its gas-plasma mix.

             

  g(r) — the intensity of the gravitational field, depending on the distance of r from the center of the star;

  M_z — the weight of a star (source of gravitation);

  r — the distance from the center of a star up to the point we’re interested in;

  G_N — gravitational constant.

In our case, the object we’re interested in (the gas-plasma mix) is situated inside of the star with an internal source of gravitation — «the white dwarf».

                                                (89)  Figure № R-5.5

The calculation of intensity of gravitational field becomes complicated and consisted from two parts.

The gravitational field inside of the star as object of gravitation and the gravitational field outside of the gravitation object of, which is «the white dwarf».

Intensity g(r), outside of gravitation object is defined by the forms:

    At    r > R

Where m – the weight of gravitation source;                                            

             r — the distance from the center of the gravitation source up to the point we’re interested in;

             R — the sphere radius — gravitation source.

 The intensity of g(r) inside the gravitation object is defined by the formula

   At    r < R

Let’s define the intensity of a gravitational field inside of the star, in the gas-plasma mix volume. The intensity of a gravitational field created by «the white dwarf» can be defined by the formula:

   At    r > R_BK                                          (5.15)

Where M_BK – the weight of «the white dwarf»;

r – the distance from the center of «the white dwarf» (the center of the star) up to the point we’re interested in;

R_BK — radius, «the white dwarf».

Let’s substitute the formula (5.15) in the formula (5.12)

The intensity of the gravitational field created by the gas-plasma mix inside of the volume we’ll define by the formula:

     r < R_Z                                         (5.16)

Where M_1GP — the weight of the gas-plasma mix, including the radiation weight;

            R_Z — the star radius.

Let’s substitute the formula (5.16) in the formula (5.14)

Since the gravitation center of both sources is situated in a general point, the distance r in both cases is equal.                            

Let’s define the intensity of the gravitational field in a point we’re interested in, considering two gravitation sources.

The intensity of gravitational fields in a star g(r) changes in time since the weight of «the white dwarf» and the gas-plasma mix change in time. At the beginning of life the weight of «the white dwarf» equals to zero. Hence, the intensity of the gravitational field created by it is also equals to zero. The intensity of the gravitational field created by the gas-plasma mix will be maximal, since its weight in the initial period of a life — is maximal.

                       g_BK(r)=0;    g(r)=g_GP(r)=max,   at   τ=0

Where τ – the lifetime of a star.                                              

During the star’s lifetime, the weight of «the white dwarf» increases due to the weight of the gas-plasma mix and by the end of life it reaches maximal value.

The weight of the gas-plasma mix decreases not only due to the increase in «the white dwarf» weight, but also due to the radiation in the space.

                       g(r)= g_BK(r)+g_GP(r)=min     at   τ=max.      

Changes of weights of the star, of the white dwarf, of the gas-plasma mix, can be presented presumably in the schedule in figure № R-5.6. 

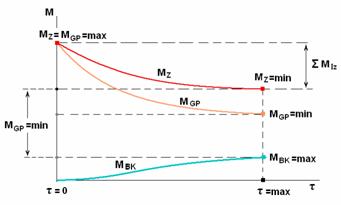
                                                            (90)  Figure № R-5.6                                                                             

Let’s deduce the formula defining the gravitational force acting on the gas-plasma mix:         

             (5.17)

                  

Where ρ_GP — the specific weight of the gas-plasma mix (which depends on g_GP(r) and r)

Let’s transform the formula (5.17)

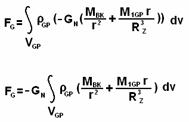        (5.18)

Let’s make preliminary, inexact calculations of the parameters for the equations of gravitational force (5.17) and (5.18) for the star «Sun».    

The physical parameters of the Sun are necessary for us in order to process the given calculation.

Let’s define the parameters of the Sun’s kernel, «the white dwarf». The radius of the Sun’s kernel doesn’t exceed more than 25 % of the Sun’s radius. Analyzing the images of the Sun received by neutrino beams (figure № R-5.4), it’s possible to calculate the radius of the Sun’s kernel. The radius of the Sun’s kernel makes 19-23 % of the Sun’s radius. We shall accept that radius of the Sun’s kernel is:

                                      R_K.Su=1.59 ^. 10⁸ m.

Let’s define the volume of the Sun’s kernel in the formula:

Let’s define the weight of the Sun’s kernel in the formula

                          M*_K.Su = ρ*_K.Su ^. V_K.Su =2.7 ^. 10³⁰  kg.