M_GP — масса газо-плазменной смеси;
           M_BK — масса белого карлика;
           M_Iz — масса излучения.
Масса излучения, относительно массы звезды мала и в некоторых выводах формул ею можно пренебречь или включить в массу газо-плазменной смеси:    M_1GP = M_GP + M_Iz
                Тогда:  M_Z = M_1GP + M_BK

Массу газо-плазменной смеси можно определить по формуле:

                             M_1GP = M_Z – M_BK                                                                       (5.13)

Подставим формулы (5.11) и (5.12), в (5.13):          

                          

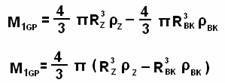
Итак, мы определили формулы для расчета основных частей звезды:

                          

                          

                                        (5.14)

Так как параметры газопламенной смеси определяют параметры звезды, нас интересует влияние гравитационного поля звезды на ее газо-плазменную смесь.

                          
           g(r) — напряженность гравитационного поля зависящая от расстояния r от центра звезды;
            M_z — масса звезды (источника гравитации);
             r — расстояние от центра звезды до интересующий нас точки;
            G_N — гравитационная постоянная.
В нашем случае интересующий нас объект (газо-плазменная смесь) находится внутри звезды с внутренним источником гравитации — белым карликом.

Так как центр гравитации, у обоих источников находится в общей точке, то расстояние r в обоих случаях одинаково.
Определим напряженность гравитационного поля в интересующей нас точке с учетом двух источников гравитации.

Напряженность гравитационных полей в звезде g(r) изменяется во времени, так как изменяются во времени массы белого карлика и газо-плазменной смеси. В начале жизни масса белого карлика равна нулю, следовательно, и напряженность гравитационного поля, создающаяся им так же равна нулю. Напряженность гравитационного поля, создаваемого газо-плазменной смесью, будет максимальная, так как ее масса в начальной период жизни максимальна.
                          g_BK(r)=0;    g(r)=g_GP(r)=max,   при   τ=0
                                    Где τ – время жизни звезды.
На протяжении жизни звезды масса белого карлика увеличивается за счет массы газо-плазменной смеси и к концу жизни достигает своего максимального значения.
Масса газо-плазменной смеси уменьшается не только за счет увеличения массы белого
карлика, но и за счет излучения в космическое пространство.
               g(r)= g_BK(r)+g_GP(r)=min     при  τ=max.      
Изменения масс звезды, белого карлика, газо-плазменной смеси предположительно можно изобразить графиком на рисунке № R-5.6.

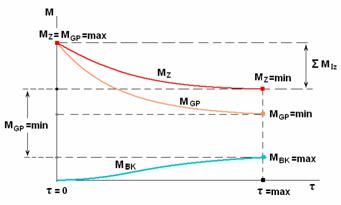
(90) Рисунок № R-5.6

Выведем формулу для определения гравитационной силы, действующей на газо-плазменную смесь:
                                                   (5.17)

                                                             

               где ρ_GP  — удельная масса газо-плазменной смеси (которая зависит от g_GP(r) и r)

                                     

Преобразуем формулу (5.17):

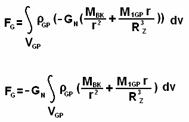                                             (5.18)

Произведем предварительные неточные расчеты параметров уравнений гравитационной силы (5.17) и (5.18) для звезды Солнце.
Для данного расчета нам необходимы физические параметры Солнца: