In case of heavier kernels, the necessary for synthesis pressure concerning a flying kernel with increase in its charge does not increase, as in case of consideration coulomb forces of pushing away, and with growth of z2 and А2 and the forces of pushing away remains almost constant due to the growth of the area of cross-section of a flying kernel. And even in case of action, the maximal coulomb forces at the synthesis moment of two kernels with z=111 and А=272 whose value reaches 8646.71 N, the necessary pressure for overcoming this force will be equaled 33.458 . 1030 Pa.
This value is lower that the necessary pressure for the synthesis of two protons 44.87893 . 1030 Pa, though the pushing away force in this case is only 90.23 N in 95.8 times is less than the pushing away force between two kernels with z=111 and А=272. Hence, in conditions of stars, the leading role at moment of synthesis, PROBABLY, played not by the coulomb forces which interfering this synthesis, and pressure which is necessary for creating on the area of cross-section of the kernels participating in this synthesis.
That means, the increase coulomb pushing away forces with the growth of quantity of protons in kernels is compensated by the increase in the area of cross-section of a kernel due to the increase in number of nucleons in these kernels.
We have considered how the will change pressure acting on a flying kernel.
But a kernel with z1 and А1 also participates in synthesis. And since it’s not mobile, it will create a pressure which interferes with the rapprochement of two kernels.
What pressure interfering synthesis, will be created by a kernel with z1 and А1?
For defining the pressure which interferes the interfering synthesis, we shall replace σ2, in the formula (2.97), with σ1 and the formula (2.95) will become:
p1=FQ/σ1 (2.98)
Where σ1 — the area of cross-section of a kernel №1 being rest.
In the formula (2.98) the schedule №G-2.15 is constructed.
(31) Schedule № G-2.15
Apparently from the schedule № G-2.15 the biggest resistance for synthesis created by a kernel of hydrogen Н with z1=1 and А1=1, that means a proton.
Hence, at the big density of a matter in a star, especially in its central part, the biggest resistance to synthesis will be rendered with kernels of hydrogen with z=1 and А=1 as the proton creates the greatest pressure of resistance to synthesis.
Apparently from the schedule № G-2.15, pressure of resistance to synthesis of kernels with the quantity of two and more nuclides is, much less, than at a proton (a kernel of hydrogen with z=1 and А=1), and even the maximal values do not exceed 35 . 1030 Pa. At synthesis of two protons pressure of resistance makes almost 45 . 1030 Pa. That above the same parameter of any other kernel of periodic system of elements (Mendeleyev).
Even if we shall take for an example reaction of synthesis of proton Р and kernels of hydrogen Н with z=1 and А=2, presence of this reaction in a star does not cause any doubt. At pressure of resistance, nearby 17.5 . 1030 Pa, we see, that kernels enter into an interval of such resistance up to a charge with Z=60 for a flying kernel, that means, that z2, and practically all kernels of a periodic table, for a based kernel z1.
It speaks for the probability of synthesis of heavy kernels.
Some researchers can object and oppose our approach concerning the analysis of pressure resistance to synthesis, instead of study of the force. And it is quite proved, in the fact of meeting of two kernels operates the pushing away force, and no matter how we represent it, whether as a kind of force, whether in the form of pressure – it is necessary to overcome it. And this reason is fair. But the force, it is lawful to consider at a meeting of two separate kernels in an environment, or in a vacuum. In that case, consideration of action of forces is unavoidable, for this variant the big barrier of pushing away exists, to avoid a chaotic synthesis of kernels in the nature. But in conditions of stars there are other conditions which we already spoke about, including the high density and compression, under the static pressure, under the influence of gravitation, and dynamic pressure, under the action of dynamic processes, at thermonuclear synthesis in the top layers of an atmosphere and radiation. And in these conditions, the consideration of synthesis of two kernels without taking into account the influence of the environment, the conditions and the forms of the star, is not correct. That’s why we consider it is necessary, to analyze not only the force interfering synthesis of kernels, but also the pressure which this force creates. So, by consideration of the influence of explosion, we shell consider not only the force, but also the pressure of a shock wave.
Let’s consider the second case when two kernels move to a point of a meeting.
In this case for overcoming the coulomb forces it is necessary to consider pressure necessary concerning the sum of cross-section of both kernels participating in the synthesis, then the formula (2.95) will become:
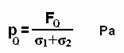 (2.99)
(2.99)
(32) Schedule № G-2.16
(33) Schedule № G-2.17
In the formula (2.99) schedules № G-2.16 and № G-2.17, from which the necessary for synthesis pressure is visible is lower, than in the first case are constructed. This decrease is received due to increase in the area of cross-section of the moving kernels. And in this case, we see, that the necessary for synthesis of two kernels pressure will be lower than a pressure necessary for synthesis of two protons. And if to take for comparison the synthesis of a proton and hydrogen Н (with z=1 and А=2) – p(p+H)=2.98 . 1030 Pa.
The maximal value of pressure necessary for synthesis of two kernels with z=111 and А=272 will be p(111+111)=16.729 . 1030 Pa, all at 5.61 time, there is more than pressure of a proton necessary for synthesis and hydrogen Н (with z=1, А=2).
And apparently from the schedule, at the moment of synthesis at easy kernels, with heavier kernels, pressure decreases. At heavier kernels it rises, but the lower pressure necessary for synthesis of two protons.
Since we are one of the first who tries to analyze the changes of pressure necessary for synthesis, and ready techniques still are not present, we shall lead the average analysis. That means in the formula (2.95) we shall substitute the average — the arithmetic area of cross-section of the kernels participating in the synthesis and the formula (2.95) will become:
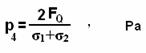 (2.100)
(2.100)