Both these of a variants are improbable. Logically speaking, the coulomb a barrier, the particle with a positive charge should overcome, and negatively charged particle breaks this barrier at leaving kernels.
There is one more variant — when the charge rotates. But even in this case overcoming full coulomb barrier is exaggerated.
Hence, the logic model of a kernel constructed under theories that are still operating in the nuclear physics is not real.
We consider, that at application of law Coulomb for kernels of atoms and the charged particles errors (mistake) have been made, which has led to divergences between the theory and the practice. We shall consider the given subject in separate analytical work. For today we should know, that there are mistakes in the theories on a structure of kernels. Hence, it is necessary for us to lean only on practically obtained data during the research.
2.4. The spherical form of stars
In this section we shall disassemble some peculiarities of the spherical form. These peculiarities increase the probability of synthesis of both easy and heavy kernels.
In the nuclear processes occurring in stars, as paradoxical as it may be, one of leading roles, and probably the most important one, is played by the spherical form of a star.
It allows to concentrate the energy allocated in a star. This surprising peculiarity of the spherical form, has made synthesis of kernels in nature possible with the most economic parameters. The form and the device of a hydrogen bomb are the clear proof of our words.
In figure № R-2.8 we see the simplicity and genius parameters of the spherical form which allows to concentrate the action of forces, from all volume, in the center of a star.
(10) Figure № R-2.8
From the figure it is visible, that the external layers of a sphere have a lot of atoms (kernels), than internal. Hence, at equal distribution of allocation of energy on the volume, concerning number of kernels, the allocation of energy will be more in layers being further from the center since with the increase in radius of a sphere, the quantity of kernels (atoms) in layers increases. Hence, allocation of energy in a sphere will work on its compression.
Let’s disassemble more in detail the scheme of figure № R-2.8.
As we see in the external layer «A» the kernels are settling down more, than in an internal layer «B». At allocation of energy, during the synthesis, impulses of kernels and radiations are directed to the opposite parties. In an external layer «A», a part of the impulses is directed outside and leave the volume as radiation. Other part of impulses is directed to the center and goes on maintenance of thermonuclear synthesis, an indemnification of a part of impulses of an internal layer «B» and compression of internal layers of the star.
The form of a sphere enables to focus the allocated energy in the direction of the center. This peculiarity allows to collect all the forces operating in the given volume and to concentrate them in a direction of the center.
The kernels which have received impulses both in a layer «A» and in a layer «B», will collide with other kernels and among themselves. If their energy will be sufficient these collisions will lead to synthesis of kernels. If for some reasons the synthesis will not occur, the energy of the impulse will be transferred to other kernels, or will pass into thermal energy.
Hence, the maximal allocation of energy in stars is in the top layers of the atmosphere.
From the stated above it is possible to draw a conclusion, that the form of a star — a sphere, transforms and strengthens power processes.
Let’s consider the influence of impulses of kernels and the radiations received at synthesis on behavior of a star, figure № R-2.9.
(11) Figure № R-2.9
As we can see from figure № R-2.9 the impulse of radiation and an impulse of kernel «C» can be spread out on axes and to define influence of impulses on processes in a star.
On axis «Y» impulses work on radiations from the external party and on synthesis and compression with internal. On axes «X» and «Z» impulses work on rotation and circulation of a matter in a star.
Probably, those different layers in a star have different directions of rotation and circulation.
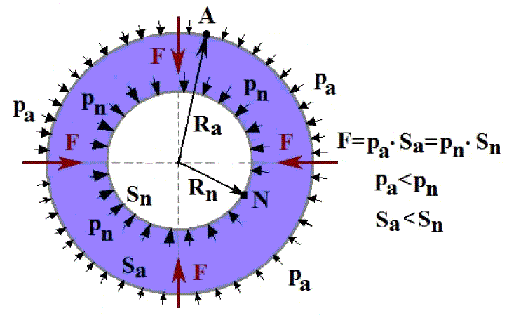
Let’s consider a sphere, consisted of gas and liquid, with radius Ra where «A» is a point on a surface of the given sphere on the figure №R-2.10.
Let’s assume that force F operates on a surface of the sphere, directed to the center. We shall define the pressure of this force in the formula:
Where, S=4 . π . R2 — the area of the surface of the sphere with radius R.
From the formula (2.28) it is visible, that at the reduction of the area of sphere S, the pressure upon the surface increases.